Hinweis:
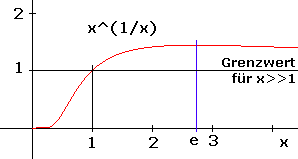
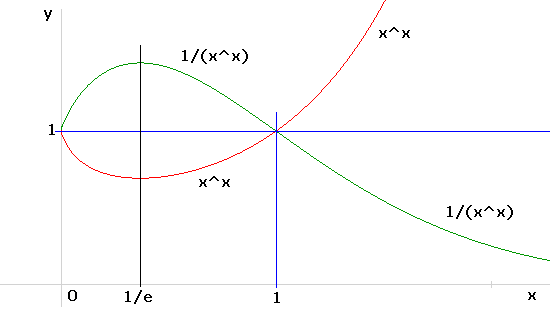
Die Funktionen x^(1/x) und x^x haben bei der Eulerschen Zahl x=e bzw. x=1/e Extremwerte:
Startwert:
x = ln(A)/2 (für A > 1000) oder x = ln(A) (für 1000 > A > e*e)
oder x = 1 (für A < e*e)
Newton-Verfahren:
Schleife: x = (x + ln(A))/(1.0 + ln(x));
Hinweis:
Die Funktionen x^(1/x) und x^x haben bei der Eulerschen Zahl x=e bzw. x=1/e
Extremwerte:


Herleitung Newton-Rekursion:
A = x^x = exp(ln(x^x)) =
exp(x*ln(x))
Erste Ableitung:
(x^x)' = exp(x*lnx) * (x*lnx)'
(x^x)' = exp(x*lnx) * (lnx + 1)
(x^x)' = x^x * (ln(x) + 1)
Newtonverfahren:
x(i+1) = x(i) - f(x(i))/f(x(i))'
f(x) = 0 = x^x - A
x = x - (x^x - A) / (x^x
* (ln(x) + 1))
x = x - (1 - A/x^x) / (ln(x) + 1)
x = x - (1 - 1) / (ln(x) + 1)
Hauptnenner:
x = ((x*(ln(x) + 1) - 0) / (ln(x) + 1)
x = (x*ln(x) + x) / (ln(x) + 1)
Ergebnis (Iterationsschleife):
x = (x + ln(A)) / (1
+ ln(x))
=============================